Este Trabalho foi realizado em parceria com meus amigos de sala, Samuel Valdomiro, Michelle negreiros e Gláucia Queiroz, espero que o conteúdo seja útil =)
Equações diferenciais
Uma equação diferencial é uma equação que sua incógnita é uma função que é apresentada na equação sob a forma das respectivas derivadas. Por exemplo, dada uma variável x em função de uma variável y, a equação diferencial envolve x, y, derivadas de y e eventualmente derivadas de x.
É importante mencionar que as equações diferenciais possuem algumas propriedades interessantes, tais como:
- A solução da equação pode existir ou não.
- E caso exista esta solução pode ser única ou não.
Outro aspecto a se mencionar sobre equações diferenciais é a ordem, onde a ordem da equação diferencial é igual à ordem da derivada de maior grau que aparece na equação. Portanto a solução de uma equação diferencial de ordem n conterá n constantes.
Equações de primeira ordem: As equações diferencias de primeira ordem são da forma F(x, y, y’) = 0, porém geralmente por meio de simples manipulação algébrica é possível reescreve-la na forma de uma ou mais equações.
Equações de segunda ordem: As equações diferenciais de segunda ordem são da forma a(x) y’’ + b(x)y’ + c(x)y = d(x), para este caso d(x) seja diferente de zero serão denominadas não homogêneas e se d(x) for igual à zero será denominada homogênea.
As equações diferenciais têm inúmeras aplicações e são usadas amplamente por modelos matemáticos ou modelos de fenômenos físicos, como por exemplo: a dinâmica de fluidos e a mecânica celeste. As equações diferenciais também são aplicadas por outros setores tais como a medicina, química, biologia, engenharia, as soluções que estas propõem são usadas em projetos importantes para a sociedade atual como, por exemplo: automóveis, aviões, pontes ou mesmo circuitos elétricos.
Tipos
Podemos dividir as equações diferenciais em dois tipos:
- A Equação diferencial ordinária (EDO): Esta contem apenas funções de uma variável e derivada daquela mesma variável.
- E a Equação diferencial parcial (EDP): Esta por sua vez contem funções com mais de uma variável e suas derivadas parciais.
Métodos de coeficientes a serem determinados
Os métodos de coeficientes indeterminados é, talvez, um dos mais utilizados procedimento para se obter uma solução particular de uma equação diferencial linear de ordem m com coeficientes constantes não homogêneos. Este método se aplica a coeficientes constantes em que o termo f(x) é um a exponencial, um seno, um cosseno ou um produto dessas funções.
Ilustraremos alguns exemplos de sua aplicação:
Exemplo 1
f(x) É uma exponencial:
y''+y'-2y=3e2x
Uma função cuja combinação linear com as suas derivadas possa gerar a exponencial é a própria exponencial. Sendo assim podemos dizer que a solução dessa EDO não homogênea terá a seguinte forma:
yp = Ae2x
O coeficiente A é obtido por substituição de yp na EDO:
4Ae2x+2Ae2x-2e2x=3e2x ⇒ A=34
Logo:
yp =34e2x.
E a solução geral da equação não homogênea será:
y= yh +yp =C1 e-2x+C2 ex+34e2x.
Exemplo 2
f(x)É um polinômio:
2y''+4y = 8x2
Se o resultado da combinação de yp com suas derivadas é um polinômio de ordem n, então yp deverá ser também um polinômio de ordem n:
yp =Ax2+Bx +C
Determinamos os coeficientes substituindo yp na EDO. Primeiro calculamos yp ’ e yp ’’:
yp '=2Ax+B
yp ''=2A
Substituindo:
2A+4Ax2+4Bx+4C=8x2
4Ax2+4Bx+(2A+4C)=8x2
4A=8 A=2
4B=0 ⇒ B=0
2A+4C=0 C=-1
Ou seja, a solução particular é:
yp =2x2-1
E a solução geral é (yhjá era conhecido):
y=C1cos(2x)+C2sin(2x)+2x2-1
Podemos nos deparar com situações em que a resolução se complica ligeiramente e teremos de adotar soluções particulares. Acontece que yp =Ae2x é uma solução de equação homogênea correspondente, logo nunca poderia ser também solução de equações não homogêneas. O Fato é que o método de coeficientes indeterminados tem uma obvia limitação, onde só podemos aplicar a equações de coeficientes constantes.
Métodos das variações dos parâmetros
A equação de segunda ordem é dada como A(x)y′′ + B(x)y′ + C(x)y = D(x), sendo suas funções contínuas com um intervalo I onde a função A(x) jamais será nula. O método de variações dos parâmetros é conhecido através de duas soluções lineares independentes y1(x) e y2(x), sendo elas EDO. Na forma homogênea, sua fórmula é: yH(x) = C1 y1(x) + C2 y2(x) e em uma solução particular yP(x) não homogenia, sua fórmula é: yP(x) = u(x) y1(x) + v(x) y2(x). Onde o u(x) e v(x) são funções a determinar, executando a condição lateral:
u′(x) y1(x) + v′(x) y2(x) = 0 (I)
Em seguida derivando duas vezes a solução yP(x), utilizando a condição lateral, chegando à solução:
y’p (x) = u(x) y’1(x) + v(x) y’2(x)
y’’p (x) = u’(x) y’1(x) + u(x) y’’1(x) + v’(x) y’2(x) + v(x) y’’2(x)
Ao substituirmos yP(x), y′P(x) e y′′P na EDO, sendo y1(x) e y2(x) solução homogênea, onde as expressões entre colchetes são iguais à zero, obtemos esse resultado:
u(x) [A(x)y′′ + B(x)y′ + C(x)y] + v(x) [A(x)y′′ + B(x)y′ + C(x) y]+ A(x)[ u′(x)y′1(x) + v′(x)y′2(x)] = D(x)
_____
u’(x) y’1(x) + v’(x) y’2(x) = D (x)/A(x) (II)
Com a combinação das duas equações (I) e (II) teremos o sistema linear:
O determinante principal se trata do wronskiano w(y1, y2) das soluções y1(x) e y2(x), que não é nulo. Usando a regra de Cramer ou outra maneira de calcular u′ e v′ por integração, pode- se chegar à solução yP(x).
Introdução a sequências e series infinitas
Só podemos compreender series infinitas, após entendemos o conceito de uma sequência infinita. Sequência infinita: é uma Sequência em que uma função, cujo domínio é o conjunto de todos os números inteiros positivos. Uma sequência pode ter um número finito ou infinito de termos; uma sequência finita ou uma sequência infinita. É impossível enumerar ou explicitar todos os termos de uma sequencia infinita. sequências infinitas são dadas listando-se seus primeiros termos e colocando um sinal de reticências donde, se depreende a regra formadora do restante da sequência.
Sequências finitas
Números primos entre 2 e 29 (2, 3, 5, 7, 11, 13, 17, 19, 23, 29); (1°, 2°, 3°, 4°, 5°,..., 20°).
Sequências infinitas
Números naturais (0, 1, 2, 3, 4, 5,...); O conjunto entre todos os números primos (2, 3, 5, 11, 13, 17, 19, 23, 29, 31, 37,..); O conjunto de todos os números pares (2, 4, 6, 8, 10, 12, 14, 16, .)
Definição: Limite de uma sequência
A sequencia {an} tem um limite L se para qualquer ² > 0 existe um numero N > 0 tal que se n for inteiro e se n > N entao |an − L| < ².
A soma infinita a1 + a2 + a3 ++... + an + ... = é chamada série.
Cada número ai é um termo da série;
an é o termo genérico de ordem n.
Para definir a soma de infinitas parcelas, consideram-se as somas parciais.
S1 = a1
S2 = a1 + a2
S3 = a1 + a2 + a3
------------------------
Sn = a1 + a2 + a3 + ... + an-1 + an
Sequência de soma
S1, S2, S3,..., Sn,...
Se essa sequência tem limite S, então a série converge e sua soma é S. Então a série converge e sua soma é a1+a2+a3+...+an... = S
Se a sequência {Sn} não tem limite, a série diverge.
Aplicações das sequencias e series
Sequencias e series possuem inumeras aplicações na resolução de problemas, geralmente na maior parte dos casos, precisamos modelar o problema para usar os resultados conhecidos a cerca de sequencias e series. Além disso, limites no infinito podem ser usados para comparação de eficiência e complexidade de algoritmos, somas parciais de séries podem representar aproximações de integrais, entre outras aplicações. A seguir alguns exemplos em que podemos aplicar sequências e series. Sendo que dois exemplos clássicos das aplicações de sequencias e series seja na resolução de complexidade de algoritmos e equações integrais.
Sequências
Uma sequência se define como qualquer conjunto organizado de objetos, números ou mesmo eventos de qualquer natureza.
Na matemática definimos sequências como uma lista ou conjunto de números, dotados das seguintes características:
- Todos os elementos são do mesmo tipo;
- Os elementos são denominados como termos;
- Cada termo possui posição definida dentro da sequencia;
- Cada posição é denominada por um numero natural em um índice;
- Cada termo possui um único índice e cada índice pertence a um único termo
- Dois termos podem ser permutados se os seus respectivos índices também forem
Tipos
Podemos mencionar os seguintes tipos de sequências:
- Sequências monótonas;
- Sequências limitadas;
- Sequências finitas;
- Sequências infinitas.
Series
O conceito de série surgiu da tentativa de generalizar o conceito de soma para uma sequência infinita de termos, porém durante essa tentativa foram deparados alguns problemas:
- Nem sempre é possível definir um valor resultante da soma para uma série;
- Não é possível em geral trocar a ordem dos termos;
- Algumas séries possuem soma infinita.
Podemos considerar um exemplo simples para entendermos melhor as séries, como no caso da dizima periódica que é resultante da divisão de 1 por 3:
1 / 3 = 0,3333.....
Podemos reinterpretar essa dizima na forma da soma da série:
0,3 +0,03 + 0,003 + 0,0003 ......
Sendo assim podemos dizer que a soma desta série é 1 / 3.
Notação
No caso a1, a2, a3……. os termos da sequência que desejamos somar. A soma S da série será:
Chamamos de soma parcial até o termo N, SN a soma dos N primeiros termos de uma série.
Teste de convergência
Teste 1:
O Teste 1 é usado para comprovar que uma série é divergente. Exemplo:
Teste 2
O Teste 2 é de comparação, ou seja, para:
1. Se temos:
2. Se temos:
Teste 3
Sendo f: [1, + ∞) → R contínua, decrescente e positiva, onde f(n) = an.
Obtemos:
1. Sendo a integral imprópria 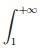 f(x) dx converge, então
f(x) dx converge, então 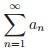 converge também.
converge também.
2. Sendo a integral imprópria 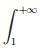 f(x) diverge, então
f(x) diverge, então 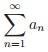 diverge também.
diverge também.
Figura x(numero): Gráficos de f(x) e f(n) = an
aiecp.files.wordpress
Teste 4
Sendo:
1. Se L < 1, a série converge.
2. Se L > 1, a série diverge.
3. Se L = 1, o teste é inclusivo.
Teste 5
Sendo alternada a série:
Seja:
1. an ≥ an +1 para todo n ≥ 1
2.
Teste 6
Sendo 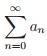 e
e 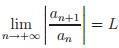 , obtemos:
, obtemos:
1. L < 1, a série  converge totalmente.
converge totalmente.
2. L >1, a série 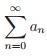 diverge.
diverge.
Bibliografia
WIKIPÉDIA. Equação diferencial, Disponível em: http://pt.wikipedia.org/wiki/Equa%C3%A7%C3%A3o_diferencial Acesso em 14 de maio de 2014.
SODRÉ U. Ensino superior: EDO de segunda ordem, Disponível em: http://pessoal.sercomtel.com.br/matematica/superior/edo/edo2ord.htm Acesso em 14 de maio de 2014.
PROF. DR. MATOS M. P. Séries e equações diferenciais ordinárias, Disponível em: http://matematicaufsj.files.wordpress.com/2012/12/caderno_calc2_vol2.pdf Acesso em 19 de maio de 2014.
Profª. DRª. PAULO G. S. Sequências e séries, Disponível em: http://www.ime.unicamp.br/~dominguez/Sequencias%20e%20Series.pdf Acesso em 19 de maio de 2014.
PROF. OURIQUE L. E. Aplicações de sequências e séries, Disponível em: http://www.pucrs.br/famat/luizedu/calculoIII/algoritmos_complexidade.pdf Acesso em 21 de maio de 2014.
FREITAS G. S. Sequências, Disponível em: http://www.infoescola.com/matematica/sequencias/ 21 de maio de 2014.
WIKIÉDIA. Série (matemática), Disponível em: http://pt.wikipedia.org/wiki/S%C3%A9rie_(matem%C3%A1tica) Acesso dia 21 de maio de 2014.
VILCHES. M. A. Equações diferenciais: métodos e séries, Disponível em: http://aiecp.files.wordpress.com/2012/07/calculo4.pdf Acesso em 21 de maio de 2014.
Nenhum comentário:
Postar um comentário